在高频下的性能，然后学习如何使用等延迟网络来提高其带宽以及如何重新设计电路以获得更高的阻抗变换比。

　　本系列的上一篇文章介绍了两个版本的Ruthroff1:4变压器-一个是不平衡到不平衡的，另一个是巴伦-通过简化分析解释了它们的低频操作。然而，在高频下，我们使用的分析方法不适用。相反，我们需要使用传输线方程式来全面了解电路的行为。

　　在这篇文章中，我们将检查一个更为严格的分析Ruthroff1:4变压器。然后我们将使用分析结果来解决这些电路与Guanella变压器相比的主要缺陷，即它们的带宽更低。在我们学习如何构建具有改进带宽的Ruthroff变压器之后，我们将学习如何构建具有更高变换率的配置。

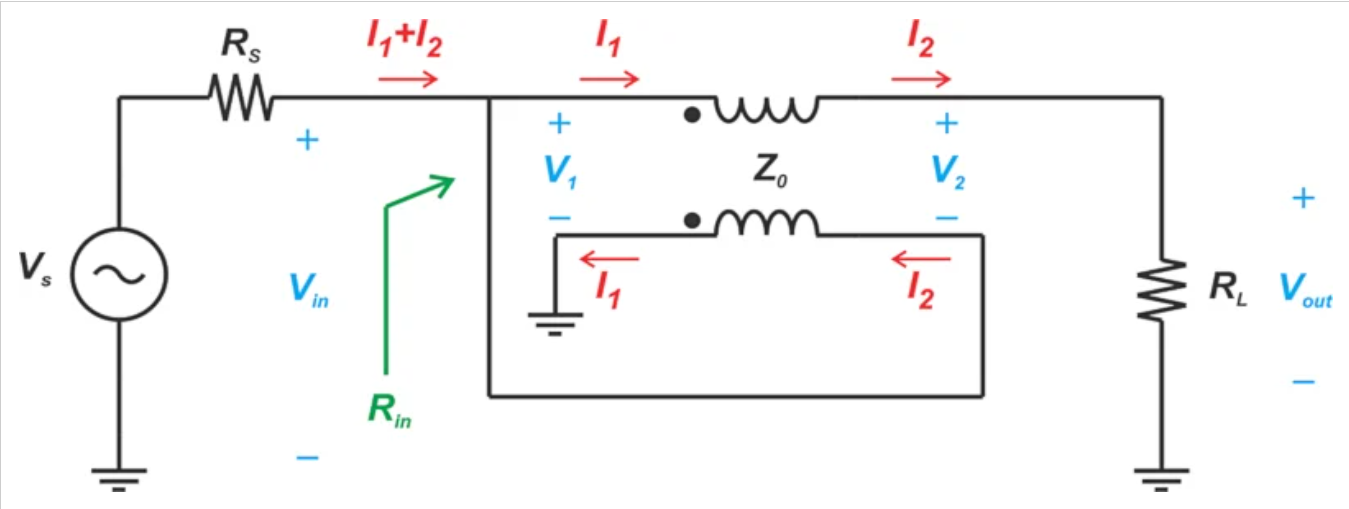
　　在低频运行时，我们可以假设传输线变压器的行为就像一个磁耦合的变压器，并使用集总电感方法进行分析，这样我们可以快速确定电路的阻抗变换比。然而，这种分析并没有揭示任何可能由非理想性施加的限制，例如线路的非零延迟。

　　为了解决这些非理想问题，我们需要进行输电线分析。假设传输线是无损的，其ABCD表示通过以下方程式描述线响应：

　　上述四个方程式包含四个未知值：V1、V2、I1和I2。求出输出电流后，我们可以计算输送到负载的功率：

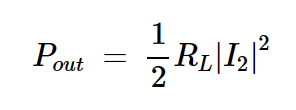
　　我们现在可以研究Pout如何随不同参数变化，以找到最佳操作条件。该数学分析的结果如下所示。为了简洁起见，我们将不逐一介绍中间的数学步骤。

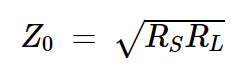
　　第二，管线的长度是受限制的——这是我们在上一篇文章中进行的简单分析中未发现的重要限制。通过求Pout对RL的导数，我们发现RL=4RS的负载阻抗最大化了输出功率。要获得这一点，线的长度必须足够小，以使βl≪1。

　　代替相位常数（β）和长度（l）的乘积，我们可以将βl看作表示电线电气长度的单个项。这让我们得出了分析的第三个重要结果，即Pout随着电线的电气长度而变化。标准化为电源（PAVS）可用功率的输出功率由下式给出：

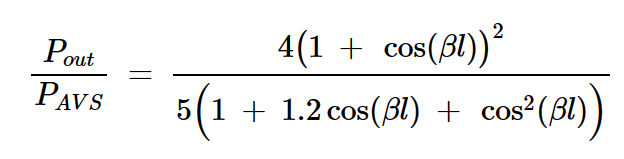
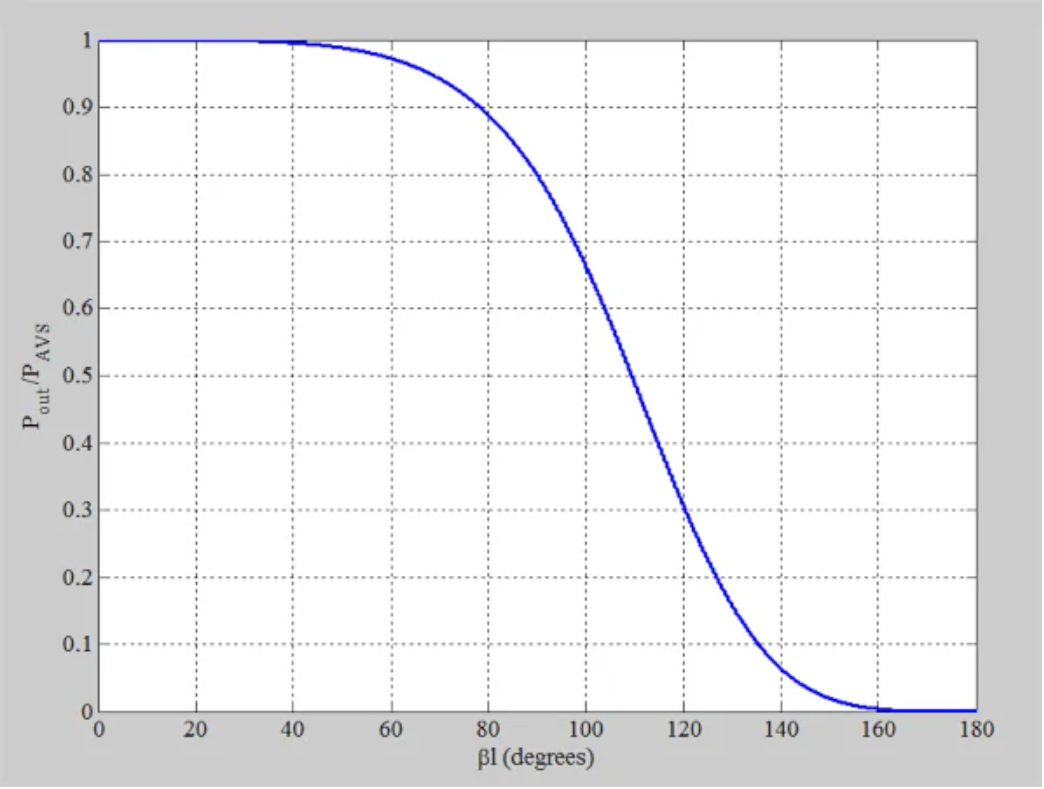
　　输出功率随着βl变大而减小，但为什么？答案在于方程式4中，方程式4告诉我们总输出电压是传输线的输入端口和输出端口处的电压之和（Vout＝V1+V2）。

　　随着相移接近180度，两个电压破坏性地干扰，从而降低了输出电压的大小。这与图2中的曲线一致，该曲线度时零输出。

　　假设¦Βl≪180度或等效地，线路的物理长度大大小于波长（l≪λ/2）的一半，则变压器按预期运行。根据经验，我们可以通过保持lλ/10来避免这种破坏性干扰。如果需要更高的精度，我们可以使用方程式7来计算给定设计的电路插入损耗的精确值。

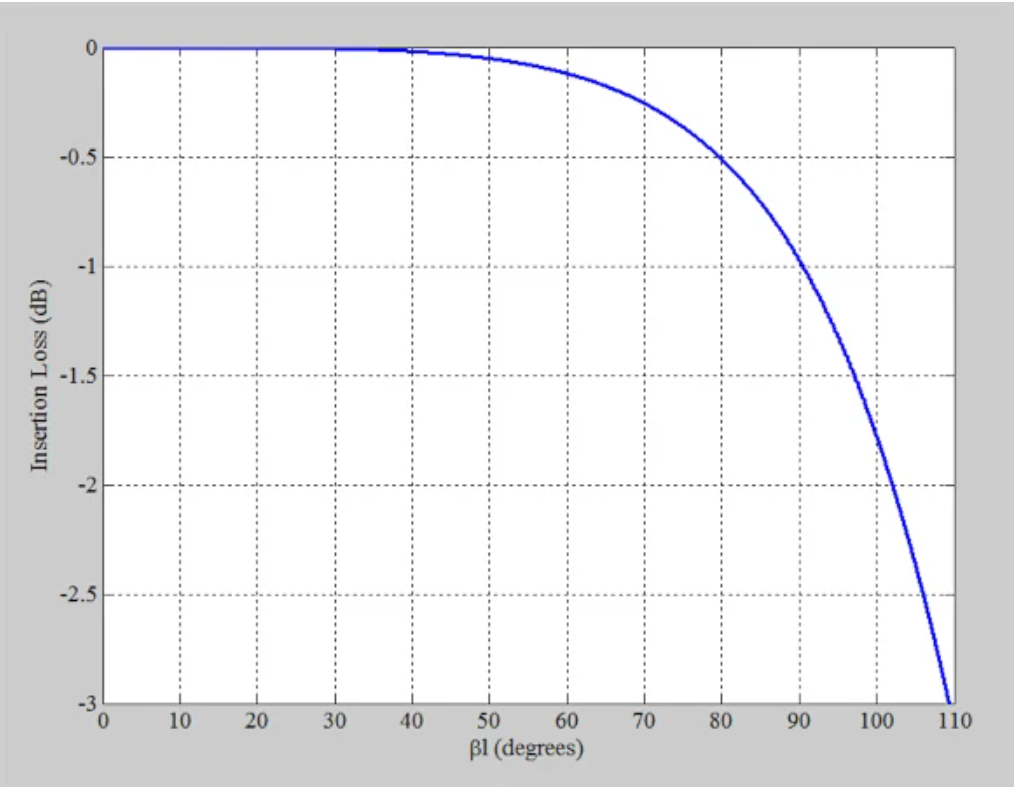
　　如果我们希望插入损耗小于0.5 dB，则电气长度不应超过80度。注意，相位常数（β）由下式给出：

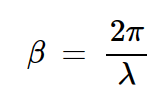
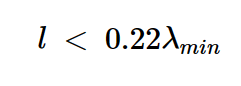
　　我们通过将电缆的速度因子乘以自由空间中的波长来找到λmin。速度因子被定义为电缆中电磁波的速度与真空中光速的比值。在我们的实例中，速度因子为0.7，得出以下方程式：

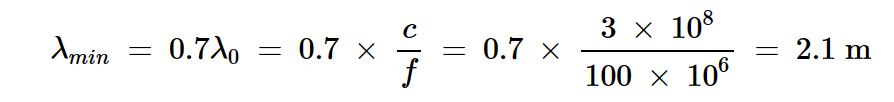
　　使用方程式9和方程式10，我们发现电缆长度不应超过46cm，以在100MHz下将插入损耗保持在0.5dB以下。更严格的插入损耗要求将进一步限制电缆长度。

　　变压器的低频响应由绕组的磁化电感确定。如果我们使线路过短，可能会阻碍我们获得所需的匝数，从而降低变压器的低频性能。

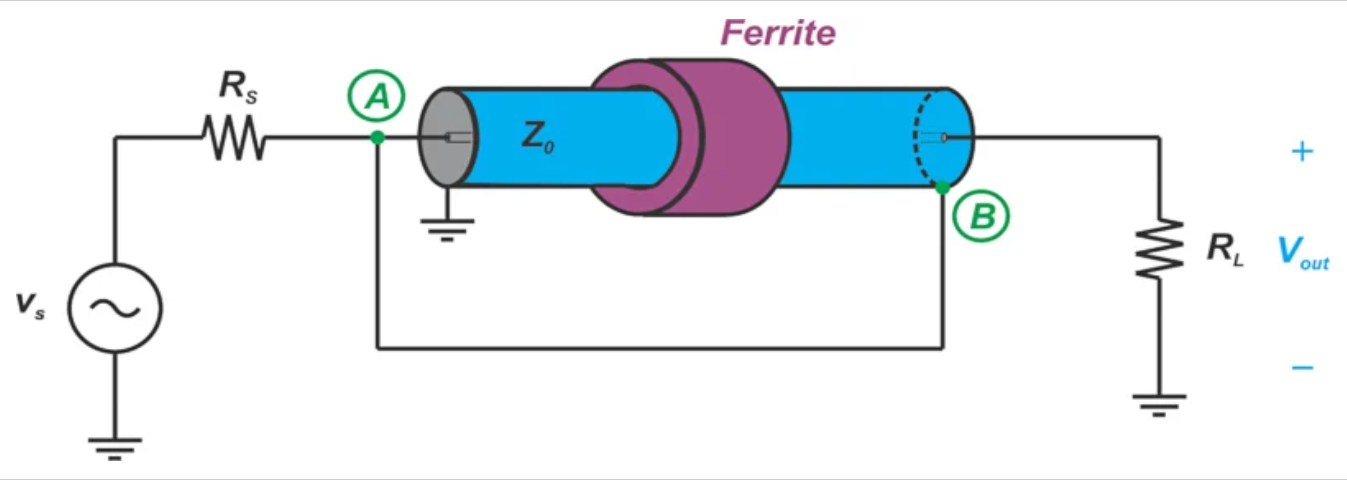
　　为了提高该变压器的高频性能，我们可以将A点和B点之间的连接实现为与干线相同长度的额外相位补偿线。这使得A到B连接的延迟也等于干线所示，被称为等延时变压器。

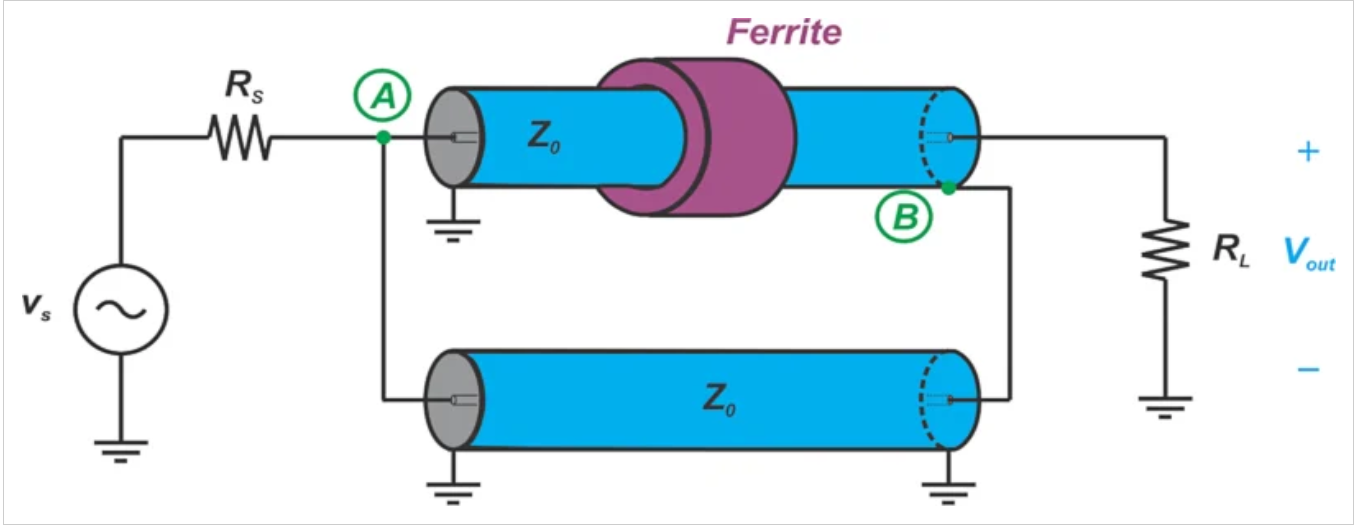
　　电路也可以被看作是两根同轴线，它们的输入端子并联，而输出端子串联。注意，只有图5中所示的变压器的上层使用铁氧体磁芯。这是因为由于两端都接地，所以在较低电线的外导体中没有电流流动。

　　我们也可以修改Ruthroff变压器，以实现1:9和1:16的阻抗变换比。图6显示了合并两条传输线阻抗转换比。

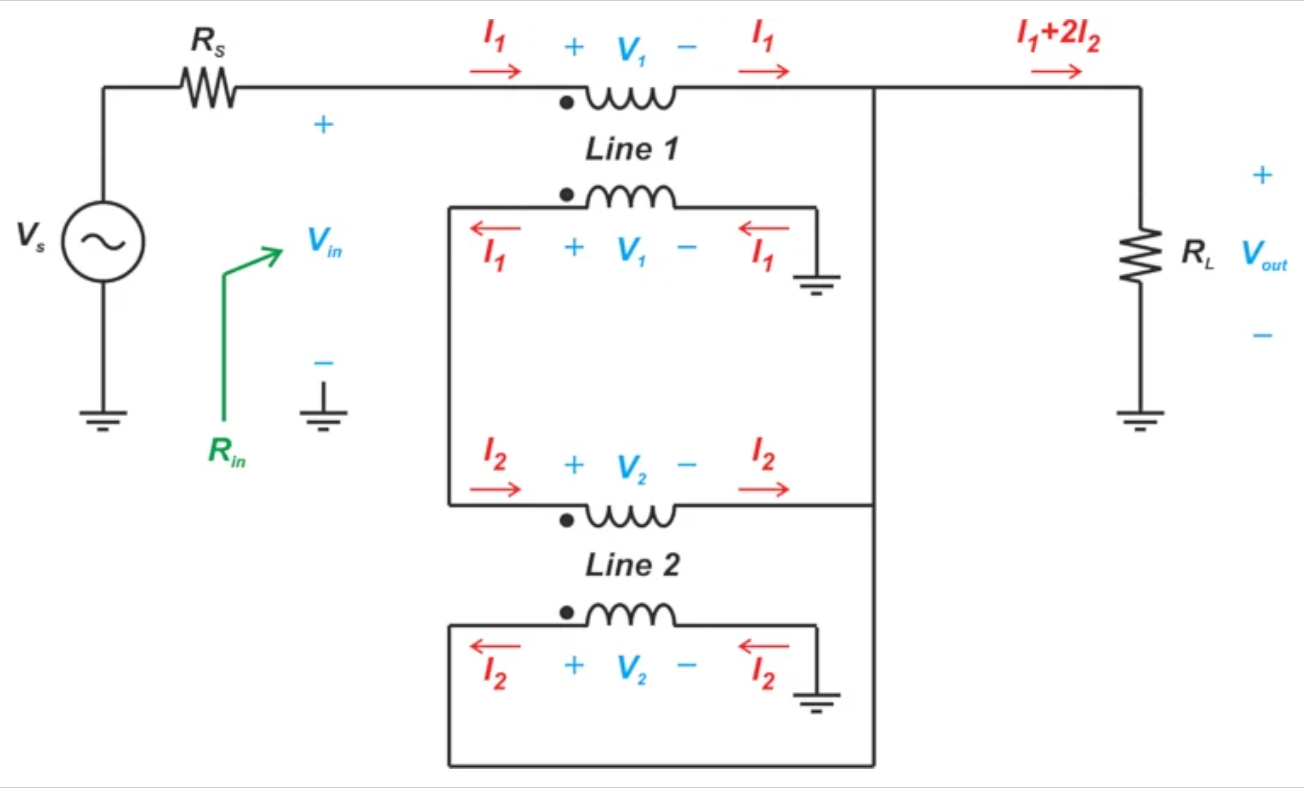
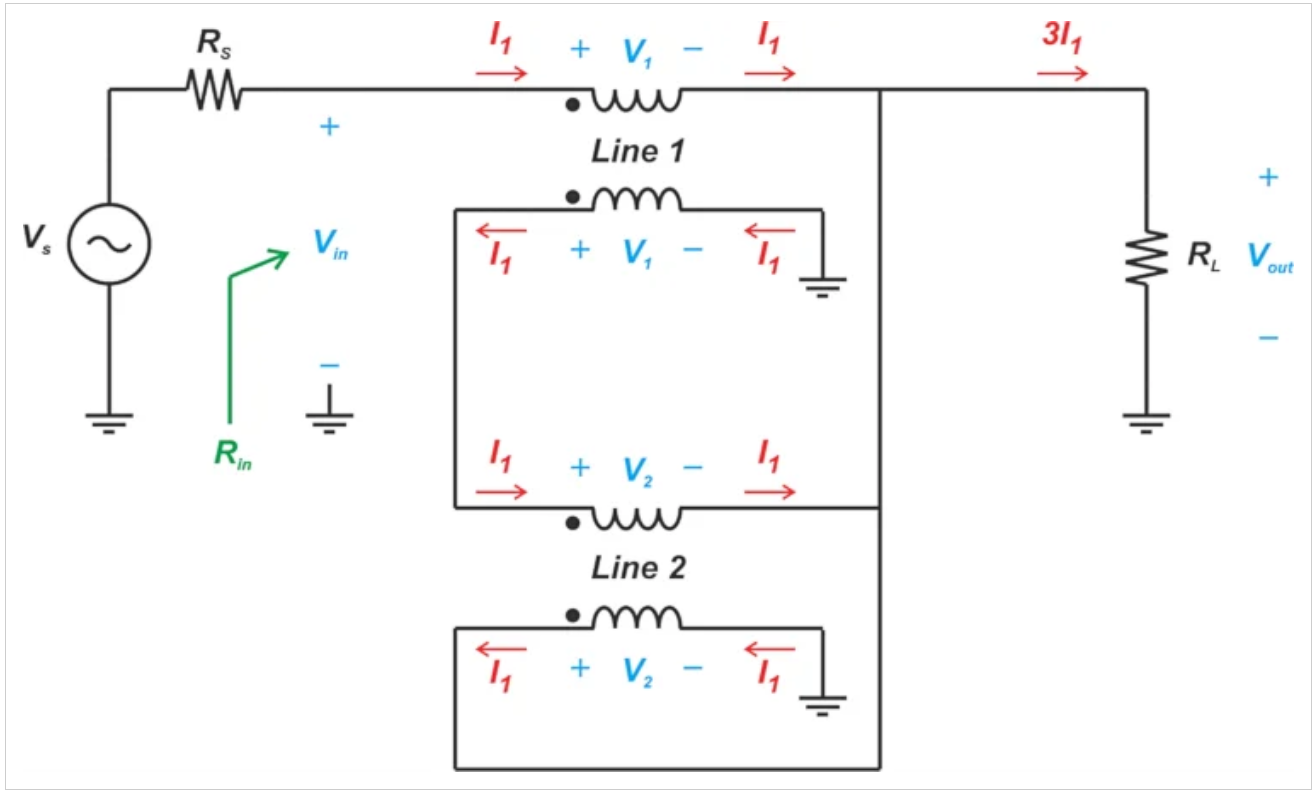
　　接下来，应用基尔霍夫电压定律，我们观察到V2＝Vout和V1＝V2+Vout＝2V2。这产生了图8中的简化示意图，其中所有电压都以V2表示。

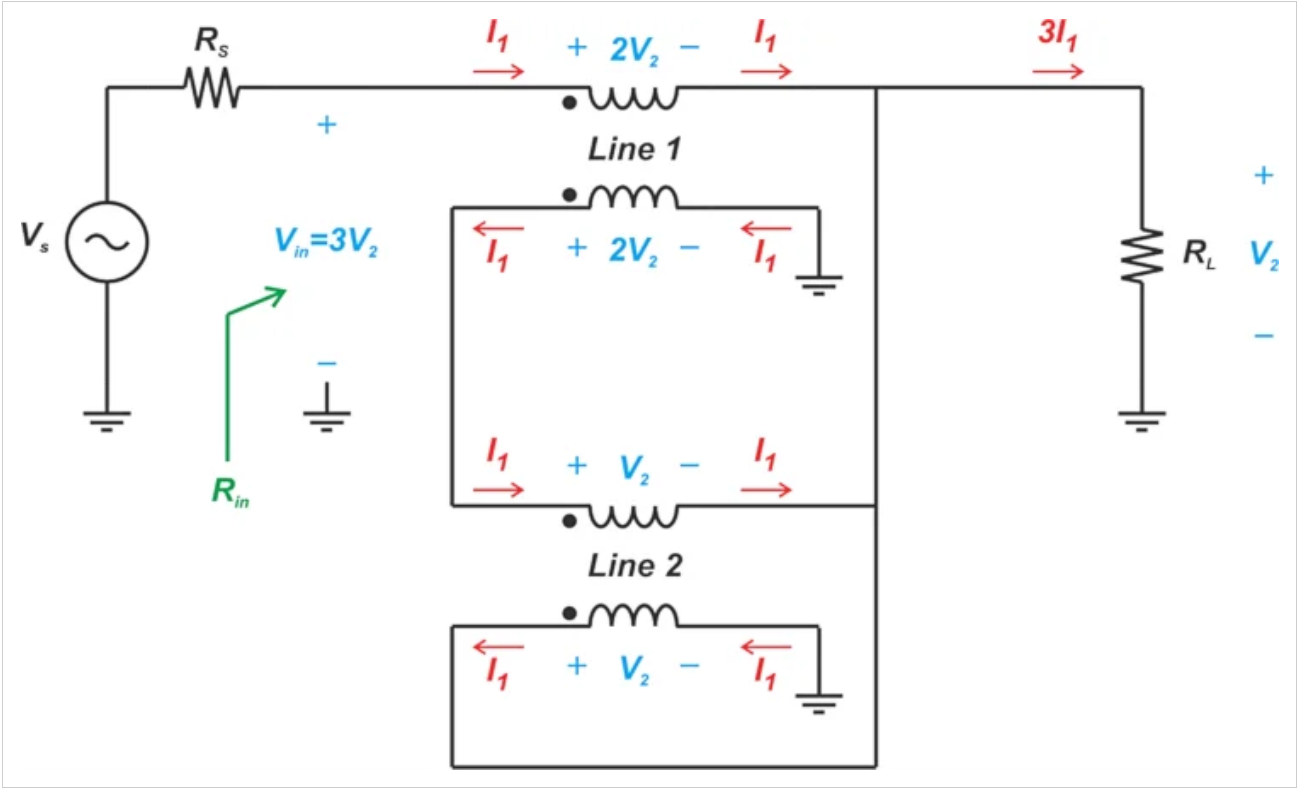
　　如上所述，输入电压为Vin＝3V2，输出电压为Vout＝V2。这表明，电路按因子3缩放电压，产生1:9的阻抗变换比：

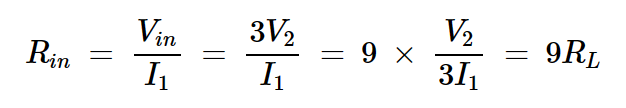
　　同样，相同的电流流过所有绕组。输出电压等于线两端的电压（Vout=V3）。当我们在网络中从一条线移动到更高的相邻线时，每条传输线。因此，这种配置中的输入电压是输出电压的四倍（Vin=4V3），对应于1:16阻抗变换比（Rin=16RL）。